Simulations of distributions
The central limit theorem is perhaps the most important concept in statistics. For any distribution with finite mean and standard deviation, samples taken from that population will tend towards a normal distribution around the mean of the population as sample size increases. Furthermore, as sample size increases, the variation of the sample means will decrease. The following examples use the R stats program to show this graphically. The first example uses a uniform (rectangular) distribution. An example of this case is of a single die with the values of 1-6. The second example is of two dice with totals ranging from 2-12. Notice that although one die produces a rectangular distribution, two dice show a distribution peaking at 7. The next set of examples show the distribution of sample means for samples of size 1 .. 32 taken from a rectangular distribution. 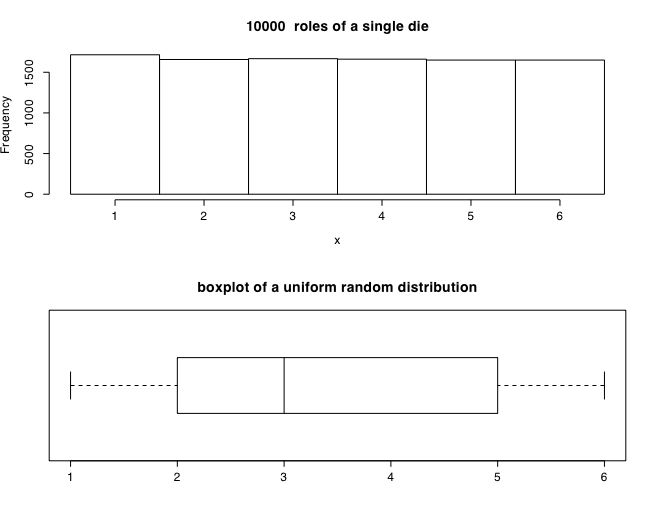
This figure was produced using the following R code.
#distributions of a single six sided die #generate a uniform random distribution from min to max numcases <- 10000 #how many cases to generate min <- 1 #set parameters max <- 6 x <- as.integer(runif(numcases,min,max+1) ) #generate random uniform numcases numbers from min to max #as.integer truncates, round converts to integers, add .5 for equal intervals par(mfrow=c(2,1)) #stack two figures above each other hist(x,main=paste( numcases," roles of a single die"),breaks=seq(min-.5,max+.5,1)) #show the histogram boxplot(x, horizontal=TRUE,range=1) # and the boxplot title("boxplot of a uniform random distribution") #end of first demo Distribution of two dice
Distribution of two dice. The sum of two dice is not rectangular, but is peaked at the middle (hint, how many ways can you get a 2, a 3, ... a 7, .. 12.). 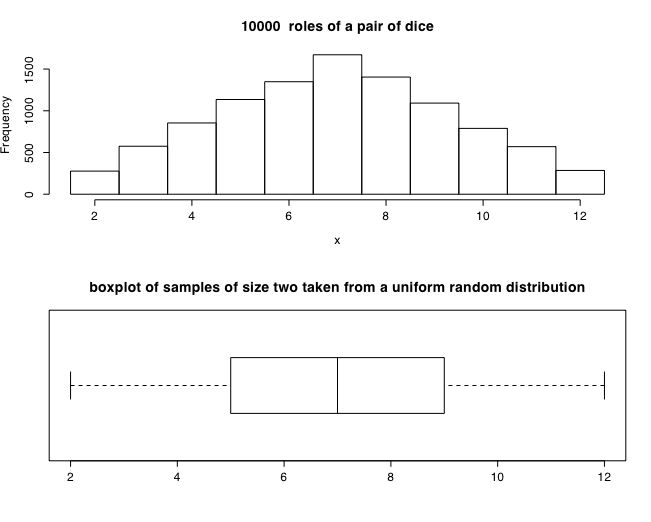
The following R code produced this figure.
#generate a uniform random distribution from min to max for numcases samples of size 2 numcases <- 10000 #how many cases to generate min <- 0 #set parameters max <- 6 x <- round(runif(numcases,min,max)+.5)+round(runif(numcases,min,max)+.5) par(mfrow=c(2,1)) #stack two figures above each other hist(x,breaks=seq(1.5,12.5),main=paste( numcases," roles of a pair of dice")) #show the histogram boxplot(x, horizontal=TRUE,range=1) # and the boxplot title("boxplot of samples of size two taken from a uniform random distribution") #end of second demo Samples from a continuous uniform random distribution
We can generalize the case of 1 or two dice to the case of samples of varying size taken from a continuous distribution ranging from 0-1. This next simulation shows the distribution of samples of sizes 1, 2, 4, ... 32 taken from a uniform distribution. Note, for each sample, we are finding the average value of the sample, rather than the sum as we were doing in the case of the dice.##show distribution of sample means of varying size samples numcases <- 10000 #how many samples to take? min <- 0 #lowest value max <- 1 ntimes <- 6 op<- par(mfrow=c(ntimes,1)) #stack ntimes graphs on top of each other i2 <- 1 #initialize counters for (i in 1:ntimes) #repeat n times { sample=rep(0,numcases) #create a vector k=0 #start off with an empty set of counters for (j in 1:i2) # inner loop { sample <- sample +runif(numcases,min,max) k <- k+1 } x <- sample/k out <- c(k,mean(x),sd(x)) #print(out,digit=3) hist(x, xlim=range(0,1),prob=T ,main=paste( "samples of size", k ),col="black") i2 <- 2*i2 } #end of i loopSome simple measures of central tendency#do the same thing, but this time show a boxplot numcases <- 10000 #how many samples to take? min <- 0 #lowest value max <- 1 ntimes <- 6 par(mfrow=c(ntimes,1)) #stack ntimes graphs on top of each other i2 <- 1 #initialize counters for (i in 1:ntimes) #repeat 5 times { sample <- 0 ; k <- 0 #start off with an empty set of counters for (j in 1:i2) # inner loop { sample <- sample +runif(numcases,min,max) k <- k+1 } x <- sample/k out <- c(k,mean(x),sd(x)) boxplot(x, horizontal=TRUE, ylim=c(0,1), range=1,notch=T) # and the boxplot i2 <- 2*i2}
#Demonstration of the effect of sample size on distributions #each sample is then replicated numcases times filename <- "distributions2.pdf" pdf(filename,width=6, height=9) numcases <- 10000 #how many samples to take? min <- 0 #lowest value max <- 1 ntimes <- 3 par(mfrow=c(2*ntimes,1)) #stack ntimes graphs on top of each other i2 <- 1 #initialize counters for (i in 1:ntimes) #repeat 5 times { sample <- 0 ; k <- 0 #start off with an empty set of counters for (j in 1:i2) # inner loop { sample <- sample +runif(numcases,min,max) k <- k+1 } x <- sample/k out <- c(k,mean(x),sd(x)) print(out,digit=3) hist(x, xlim=range(0,1),prob=T ,main=paste( "samples of size", k )) boxplot(x, horizontal=TRUE, ylim=c(0,1), range=1,notch=T) # and the boxplotl titles("Samples of sise ", i2 <- 8*i2} dev.off() #€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€ #choose a different type of distribution (binomial) filename <- "distributions3.pdf" pdf(filename,width=6, height=9) numcases <- 1000 #how big is the population min <- 0 #lowest value max <- 1 ntimes <- 6 par(mfrow=c(ntimes,1)) #stack ntimes graphs on top of each other i2 <- 1 #initialize counters for (i in 1:ntimes) #repeat 5 times { sample <- 0 ; k <- 0 #start off with an empty set of counters for (j in 1:i2) # inner loop { sample <- sample + rbinom(numcases, 1, .5) k <- k+1 } x <- sample/k out <- c(k,mean(x),sd(x)) #print(out,digit=3) hist(x, xlim=range(0,1),prob=T ,main=paste( "samples of size", k )) # boxplot(x, horizontal=TRUE, ylim=c(0,1), range=1,notch=T) # and the boxplot i2 <- 2*i2} dev.off() ####### #choose a different type of distribution (binomial) filename <- "distributions4.pdf" pdf(filename,width=6, height=9) numcases <- 1000 #how big is the population min <- 0 #lowest value max <- 1 ntimes <- 6 samplesize <- 2 prob <- .5 par(mfrow=c(ntimes,1)) #stack ntimes graphs on top of each other i2 <- 1 #initialize counters for (i in 1:ntimes) #repeat 5 times { sample <- 0 ; k <- 0 #start off with an empty set of counters for (j in 1:i2) # inner loop { sample <- sample + rbinom(numcases, samplesize, prob) #samples of size 2 k <- k+1 } x <- sample/k out <- c(k,mean(x),sd(x)) #print(out,digit=3) hist(x, xlim=range(0,samplesize),prob=T ,main=paste(numcases," samples of size", k," with prob = ", prob)) # boxplot(x, horizontal=TRUE, ylim=c(0,samplesize), range=1,notch=T) # and the boxplot i2 <- 2*i2} dev.off() ###### #choose a different type of distribution (binomial) filename <- "distributions5.pdf" pdf(filename,width=6, height=9) numcases <- 1000 #how big is the population min <- 0 #lowest value max <- 1 ntimes <- 6 samplesize <- 10 prob <- .2 par(mfrow=c(ntimes,1)) #stack ntimes graphs on top of each other i2 <- 1 #initialize counters for (i in 1:ntimes) #repeat 5 times { sample <- 0 ; k <- 0 #start off with an empty set of counters for (j in 1:i2) # inner loop { sample <- sample + rbinom(numcases, samplesize, prob) #samples of size k <- k+1 } x <- sample/k out <- c(k,mean(x),sd(x)) #print(out,digit=3) hist(x, xlim=range(0,samplesize),prob=T ,main=paste( numcases," samples of size", k," with prob = ", prob)) # boxplot(x, horizontal=TRUE, ylim=c(0,samplesize), range=1,notch=T) # and the boxplot i2 <- 2*i2} dev.off() ######## #choose a different type of distribution (binomial) # Set some parameters numcases <- 1000 #how big is the population ntimes <- 6 samplesize <- 1 #initial sample size prob <- .5 #probability of outcome par(mfrow <- c(ntimes,1)) #stack ntimes graphs on top of each other i2 <- 1 #initialize counters for (i in 1:ntimes) #repeat ntimes { #begin the loop x <- rbinom(numcases, samplesize, prob) #samples of size x <- x/samplesize #normalize to the 0-1 range out <- c(samplesize,mean(x),sd(x)) print(out,digit=3) hist(x, xlim=range(0,1),prob=T ,main=paste( numcases," samples of size", samplesize ," with prob = ", prob)) # boxplot(x, horizontal=TRUE, ylim=c(0,samplesize), range=1,notch=T) # and the boxplot samplesize <- samplesize*2 #double the sample size } #end of loop
####### x=c(1,2,4,8,16,32,64) #enter the x data summary(x) boxplot(x) x <- c(1,2,4,8,16,32,64) #enter the x data y <- c(10,11,12,13,14,15,16) #enter the y data data <- data.frame(x,y) #make a dataframe data #show the data summary(data) #descriptive stats boxplot(x,y) #same as boxplot(data)
No comments:
Post a Comment